Circular Motion - Accelerations

Animation illustrates the technique used to calculate accelerations in circular motion.

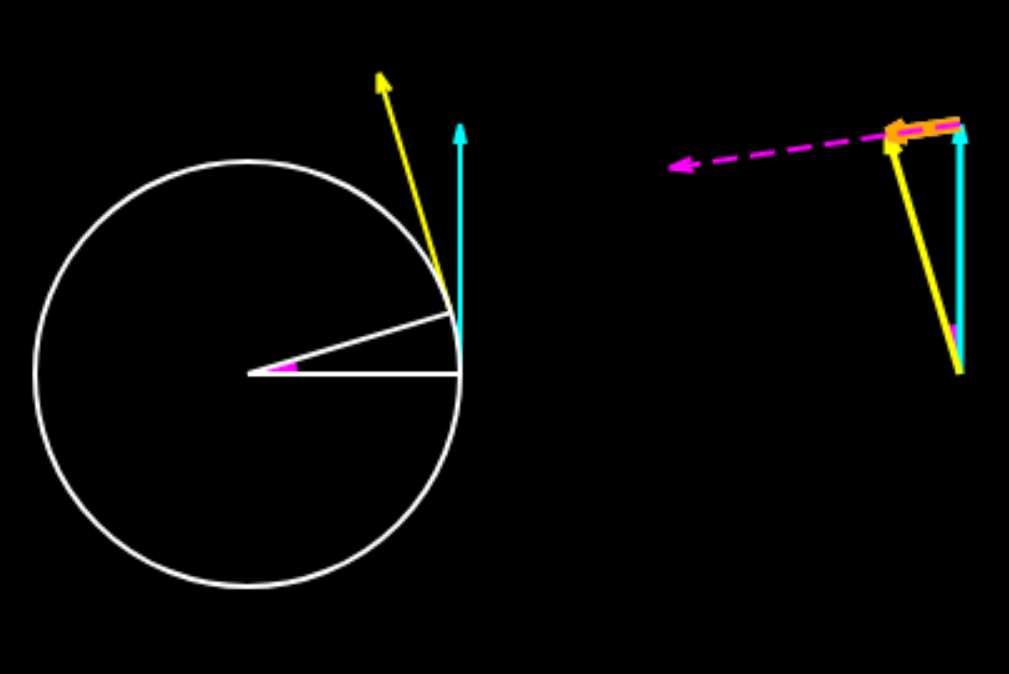
When the speed is constant the change in the velocity vector has a magnitude and the average acceleration over an interval of Δt is . This is evaluated for progressively smaller Δt.

In the animation yellow vector is the final velocity vector and the blue vector is the initial velocity vector. The orange vector has a magnitude and the magenta vector has a magnitude .

As Δt↠0 this has a magnitude rω.

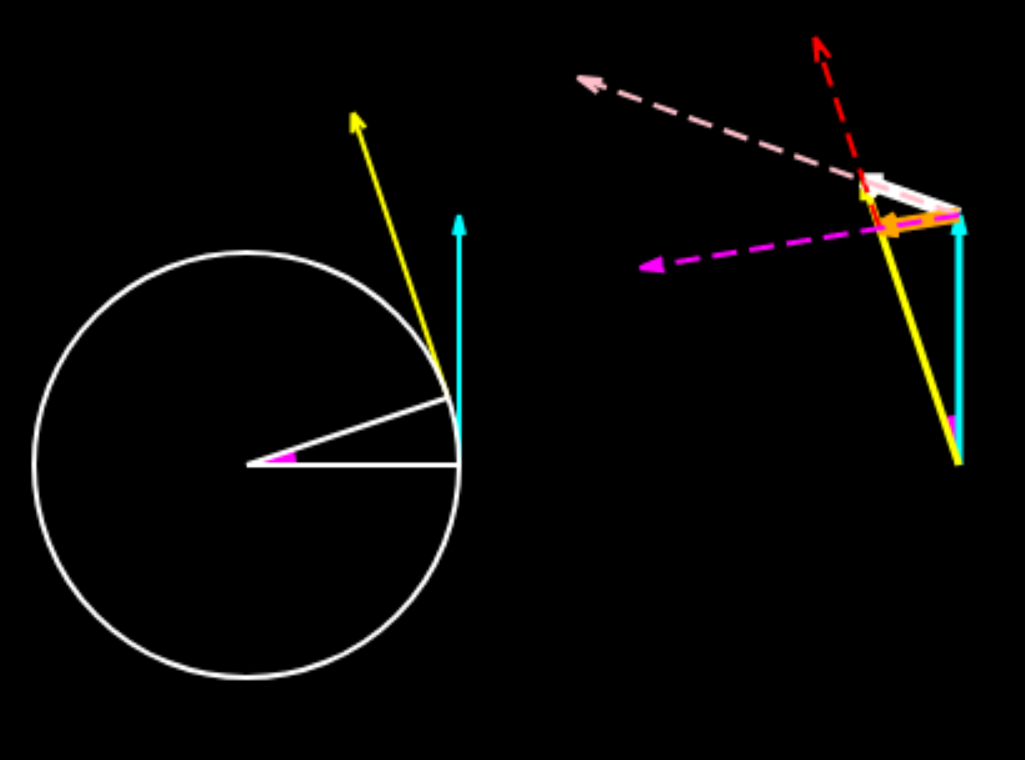
When the motion is nonuniform the yellow vector is longer than the blue vector and the white vector represents the change in the velocity vector. From the yellow vector a portion equal to the length of the blue vector is cut off and the excess length of the yellow vector over blue vector represents the change in magnitude of the velocity and this divided by the duration of time for the change gives one component of acceleration (tangential,represented by red dotted arrow). The orange vector is equal to and this divided by the duration of time gives the other component of acceleration (radial,represented by magenta dotted arrow) . The results of these calculations for progressively smaller Δt are shown. The pink vector is the average acceleration vector.