Vernier Principle
Animation illustrates the principle of Vernier calipers.
A nice tool where measurements less than that of a division of one scale are measured using two scales of different division lengths. Convince yourself that two scales of unequal division lengths can be used together to make measurements with greater accuracy.
In the Animation each main scale division is assumed to be 1 mm. It is not actually equal to that.
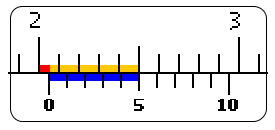
Main scale reading is the reading just to the left of the vernier zero. In the figure shown it is 2.0. Vernier coincidence is the division of vernier which coincides with one of the divisions of the main scale. It is the fifth vernier division in the figure.
Distance from one end of the object (at zero of main scale) to the coincidence point is 2.5 cm. Distance from the other end of the object (at zero of vernier) to the coincidence point is equal to five division lengths of the vernier. So the distance between the ends of the object plus the length of five divisions of vernier is 2.5 cm. The required extra fraction (red rectangle) then is the difference between five main scale divisions (from 2.5 cm to 2.0 cm, sum of the red and orange rectangles = 5 msd) and five vernier divisions (from 2.5 cm of main scale to 0 of the vernier, blue rectangle = 5 vsd. This extra fraction can then be calculated as 5*msd-5*vsd or 5(L.C.) or more generally V.C. (L.C).
If you imagine measuring from the coincidence point backwards it may be easier to see the point in using two scales. The required length can easily be seen as the difference between two measurements. One from coincidence point to 0 of main scale and the other from the coincidence point to zero of vernier. Because of the difference in the division lengths of the two scales there would be a coincidence point some where and object length plus length of some divisions of one scale will be equal to the distance up to the coincidence point from the other end of the object.
Right / Left mouse clicks move the vernier scale.

